2
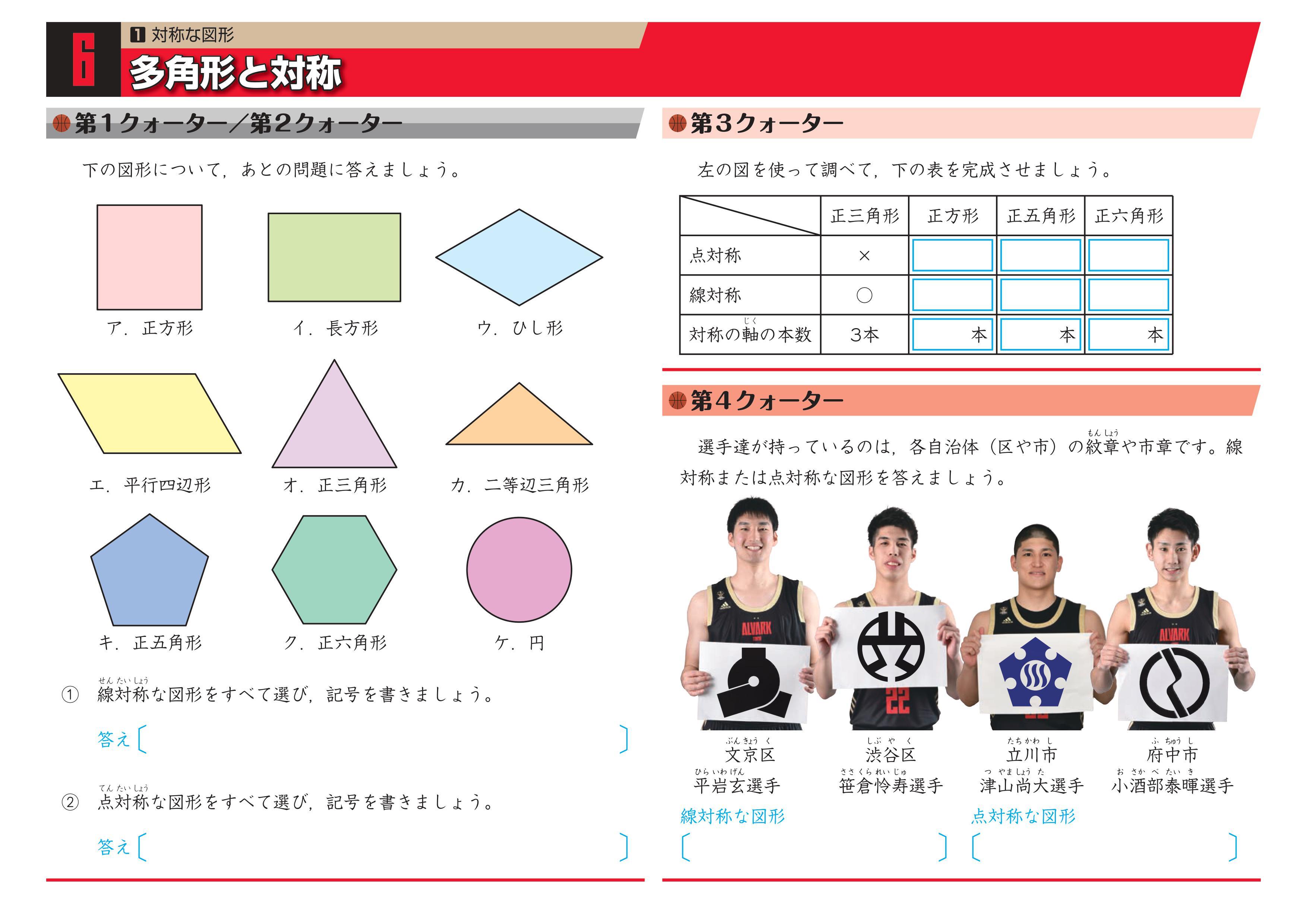
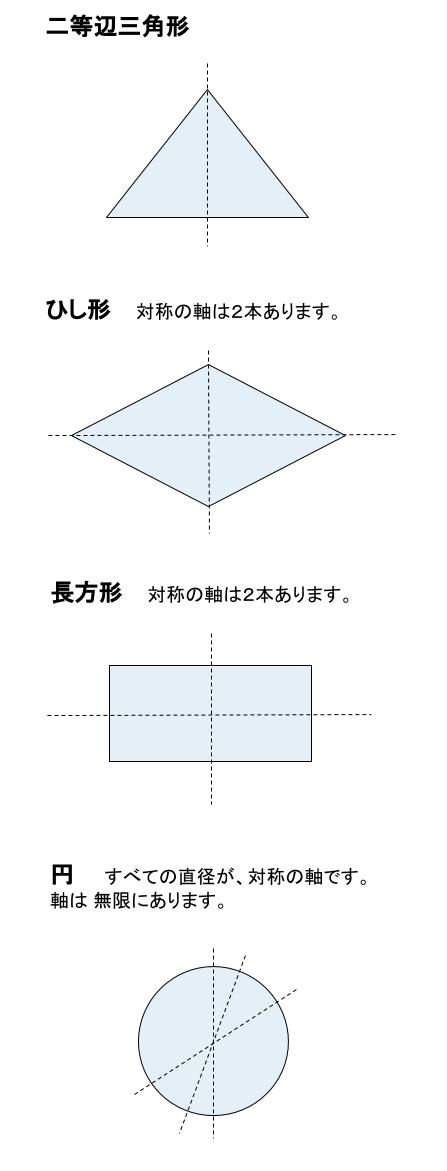
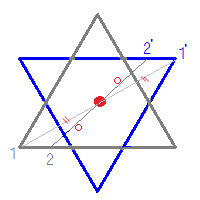
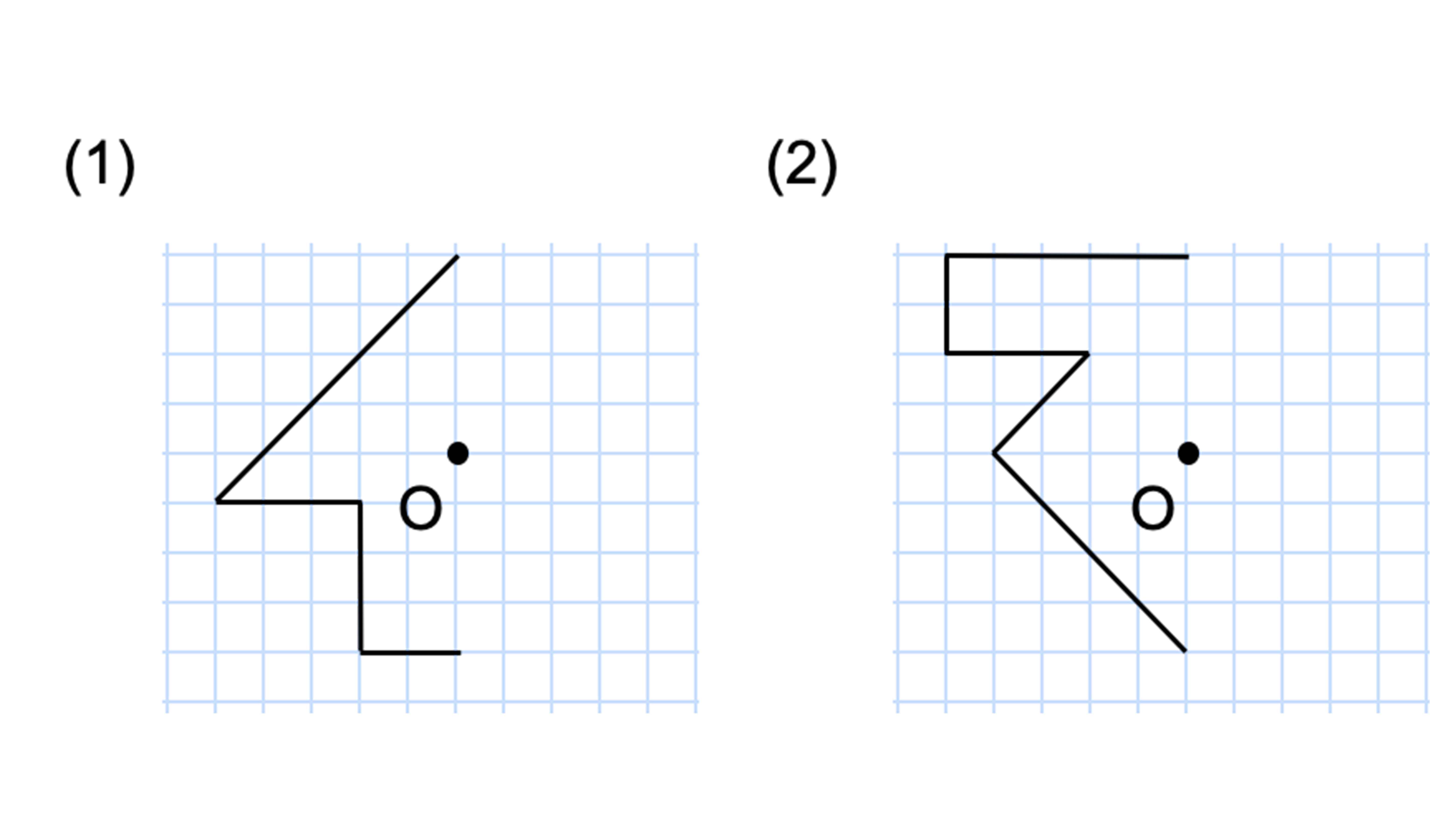
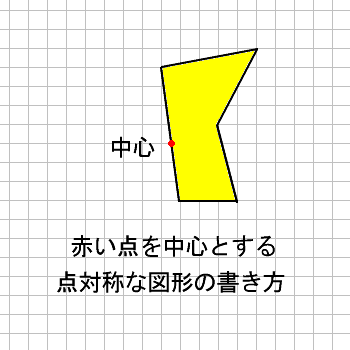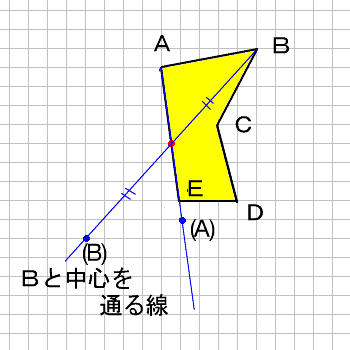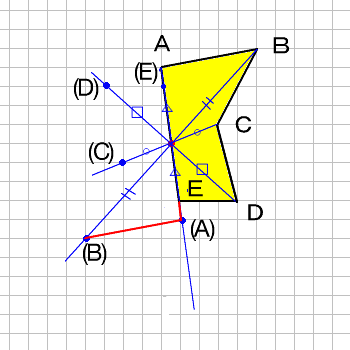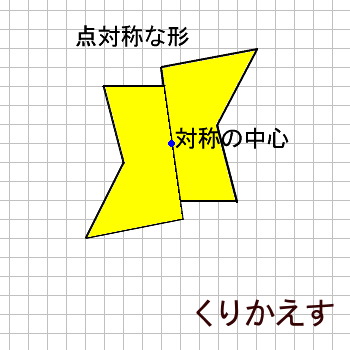
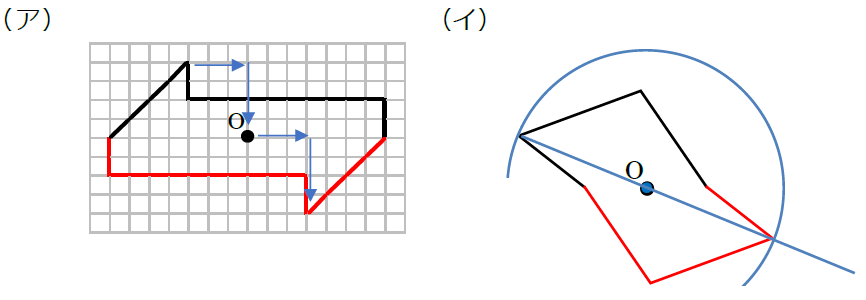
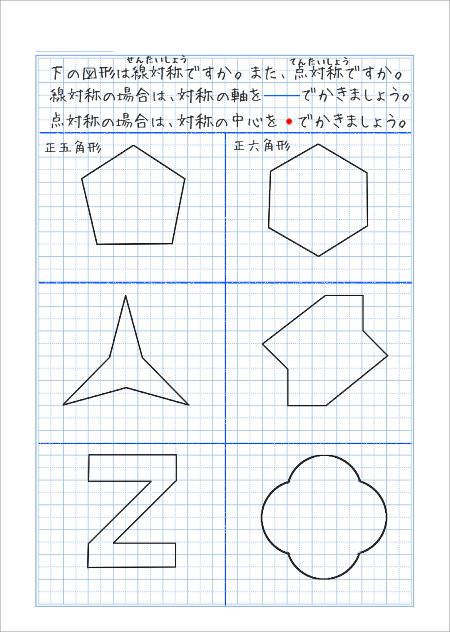
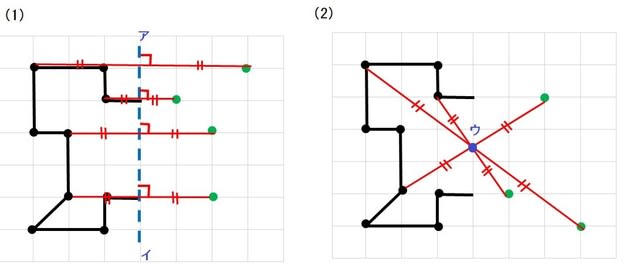
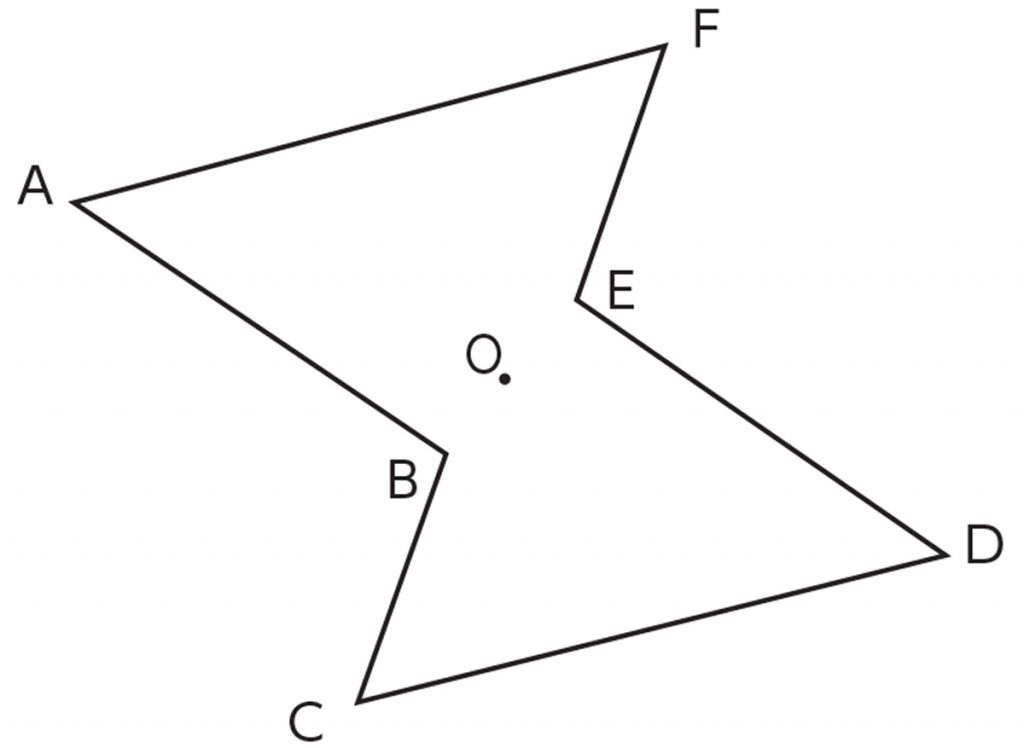
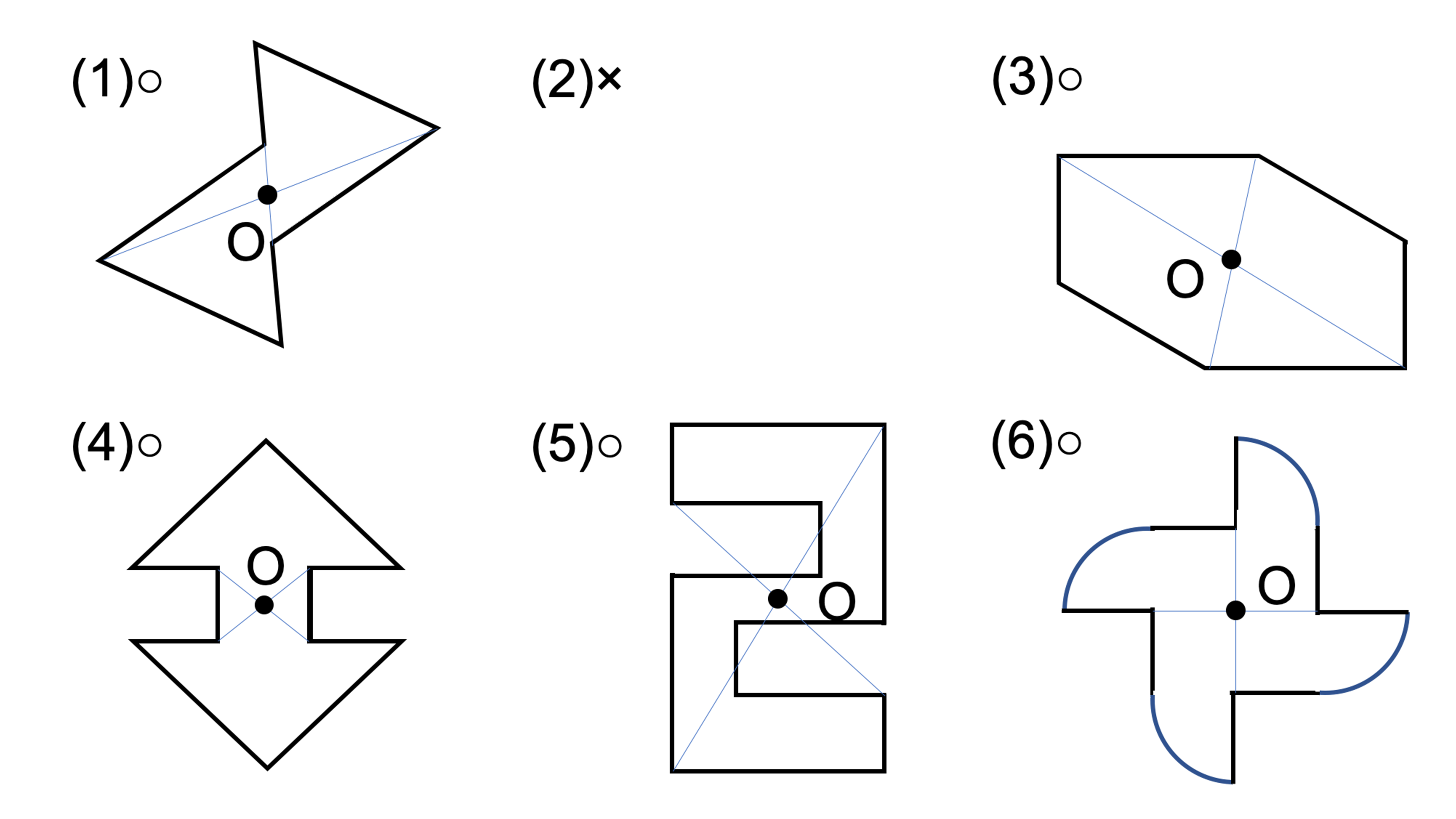
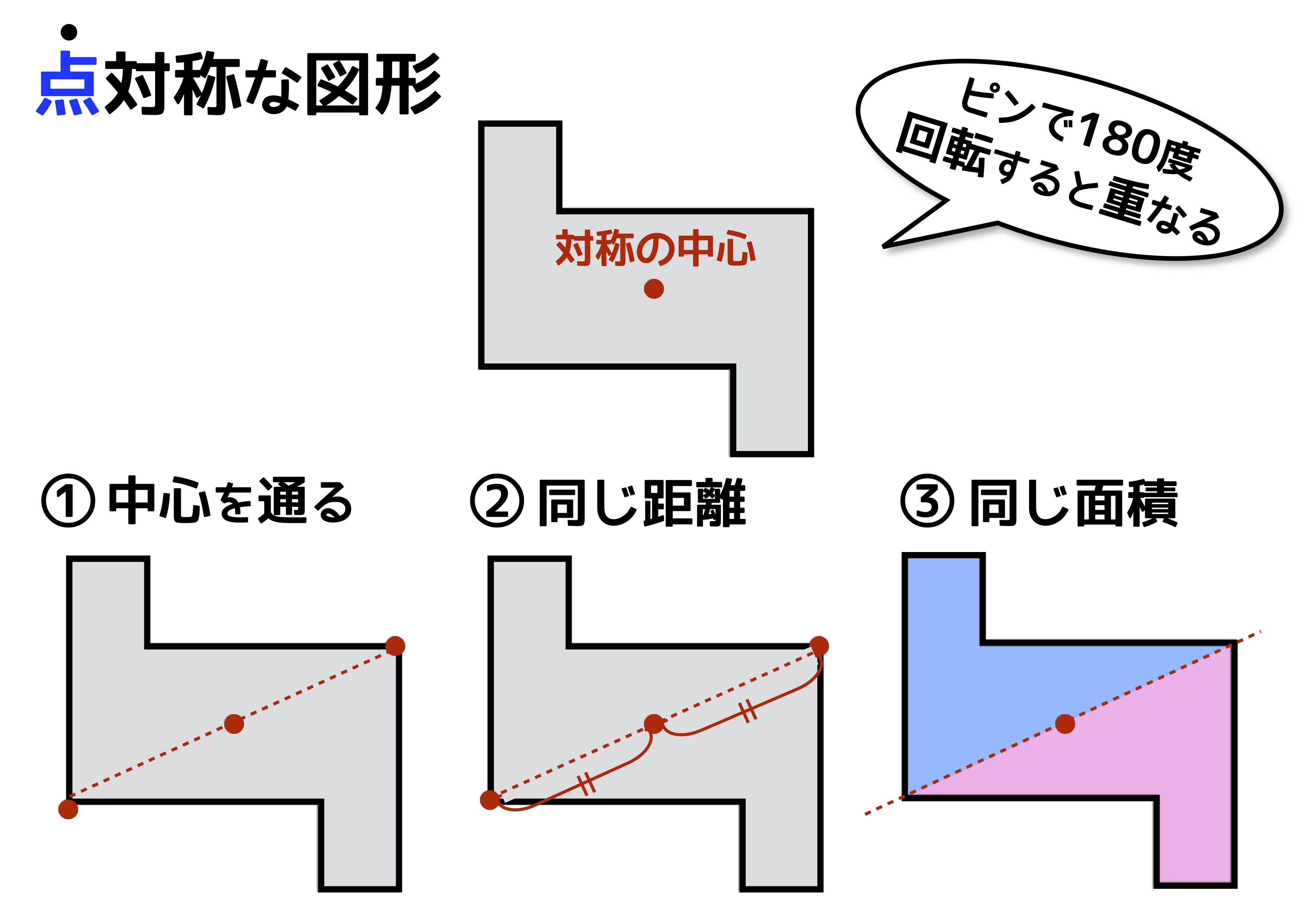
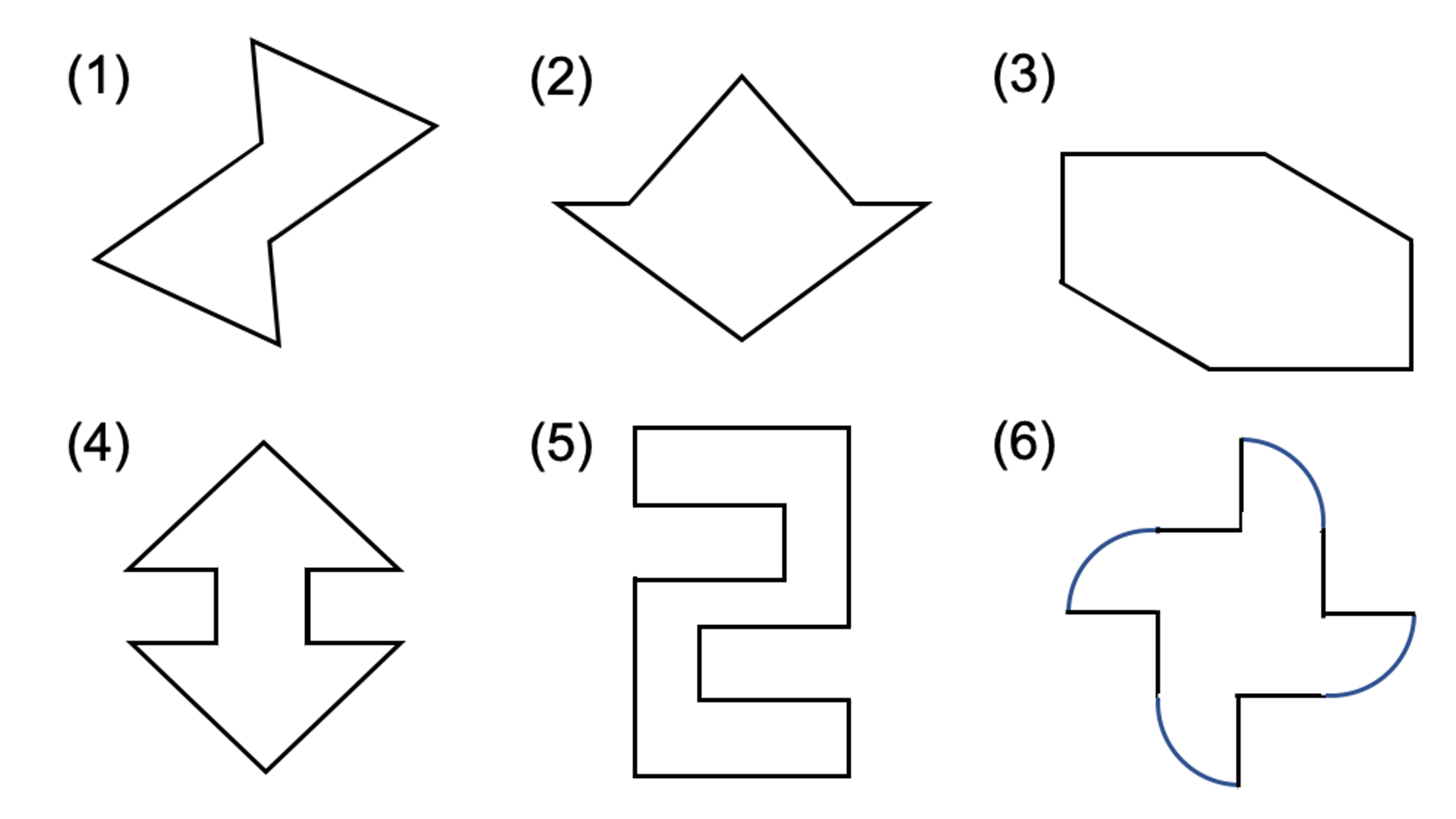
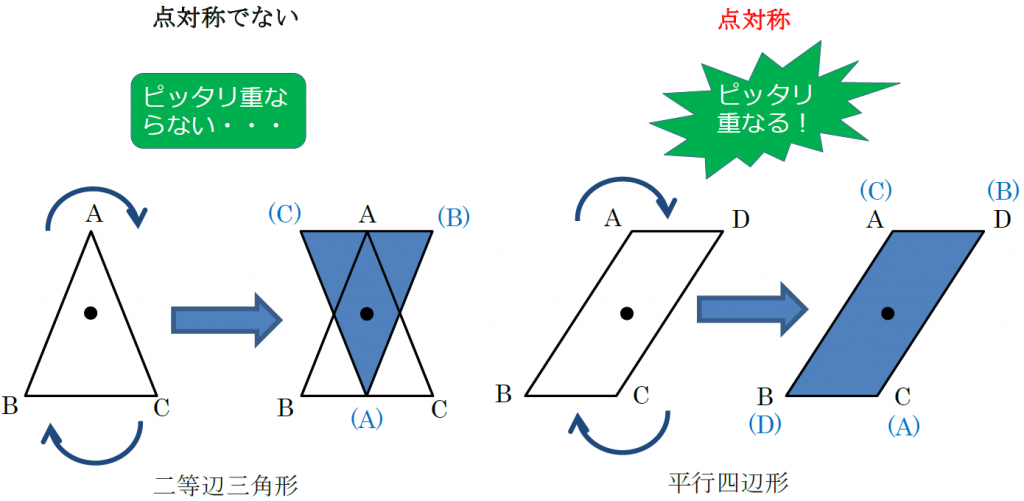
@ Ⴆ C p ` ̓_1 璆 S ܂ł̋ ” 𒆐S ̔ Α ɐL _1’ ͌ ̐ p ` ̏ ɂ C _2 璆 S ܂ł̋ o 𒆐S ̔ Α ɐL _2’ ̐ p ` ̏ ɂ D @ ̂悤 ɁC ̐ p ` i D F j 180 ƌ ̐} ` ƈ v D y T z @ p ` ͓_ Ώ̂Ȑ} ` ł͂Ȃ D 線対称かつ点対称である図形は正偶数角形だけではありません。 どの学年でも行うことのできる図形に関する授業です。隙間時間でも行えます。 問題 下の12個の図形を仲間に分けましょう。 上の図形はすべて私がwordで作成したものです。
線対称 点対称 問題
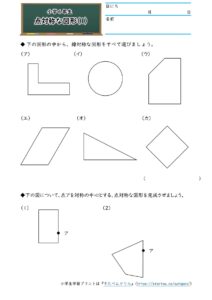
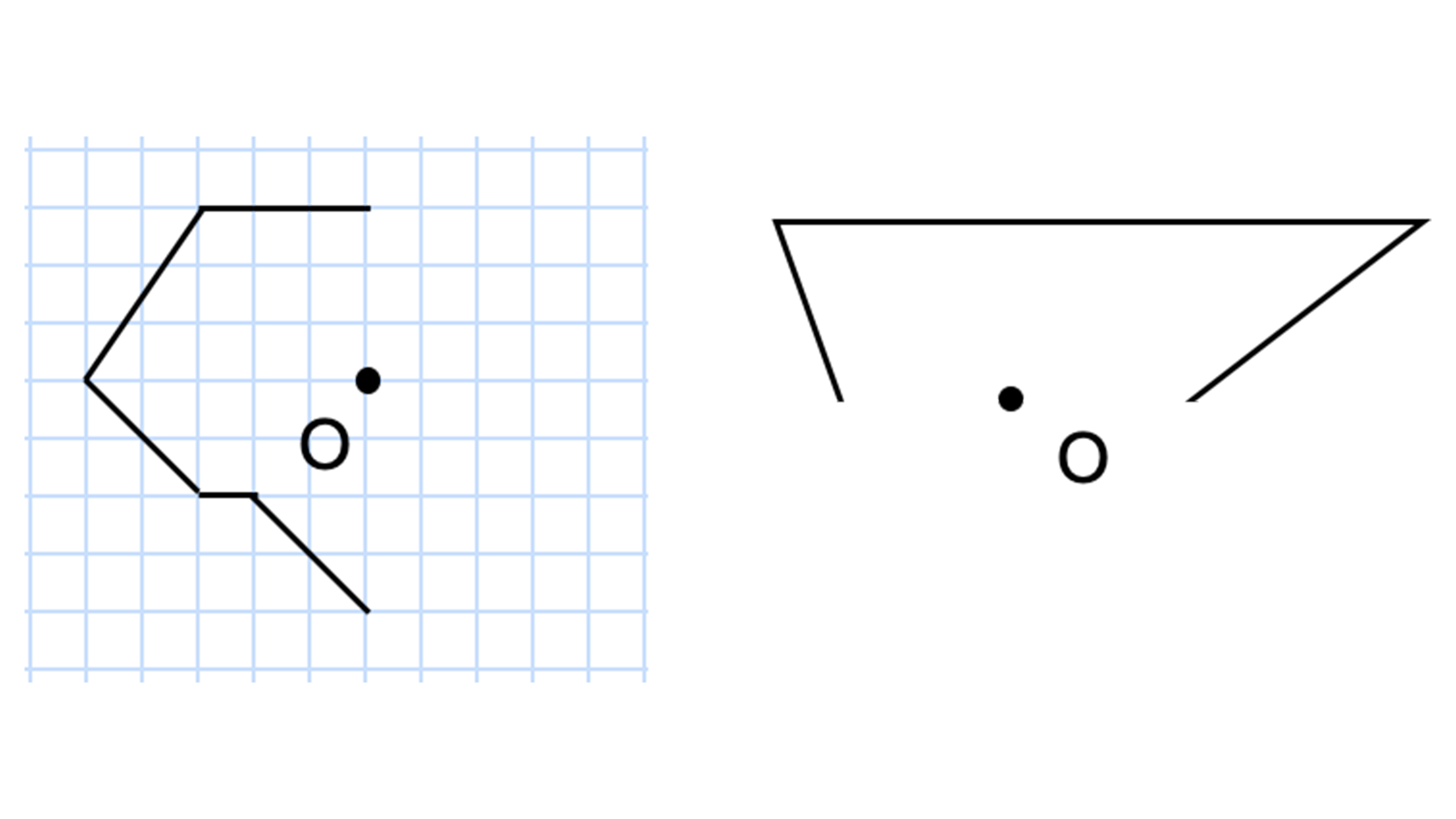
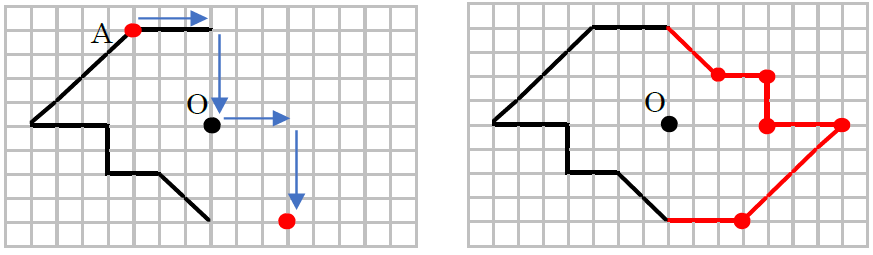
線対称 点対称 問題- 今回の問題で大切になってくるのは「 線対称 」と「 点対称 」の言葉の意味を理解して作図することです。 小学生の受験生にも分かるようにたくさんのイラストを使って解説していますので、がんばって一緒に問題を解いていきましょう!点描写 2 (線対称) 点描写とは格子状の点と点を結んで、手本と同じように図を描くことを点描写 (てんびょうしゃ)と言います。点と点を結ぶ作業は運筆の練習になると同時 に、図の位置や形を一時的に記憶することで、短期記憶の訓練にもなります。

線対称 点対称 算数用語集
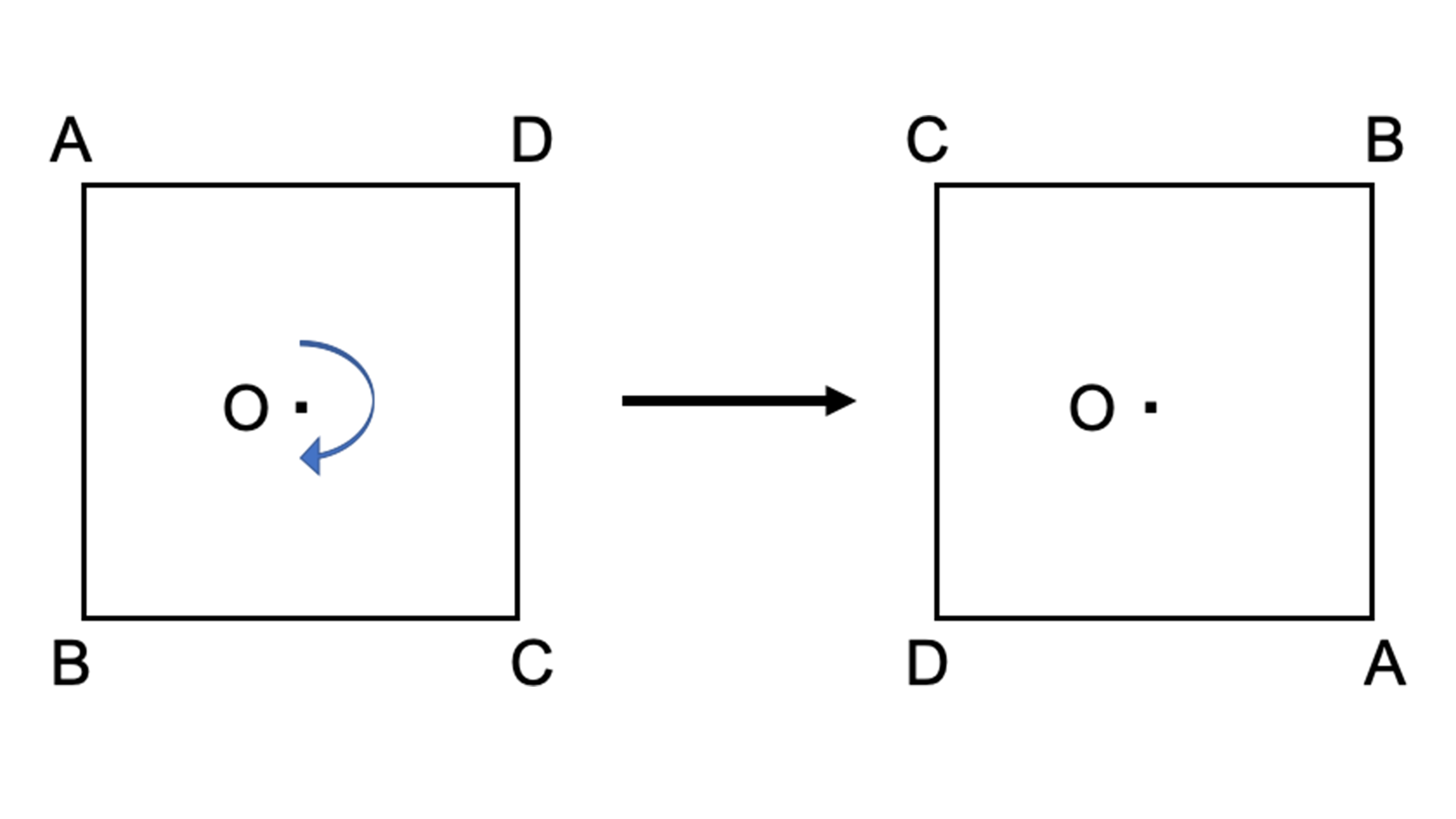
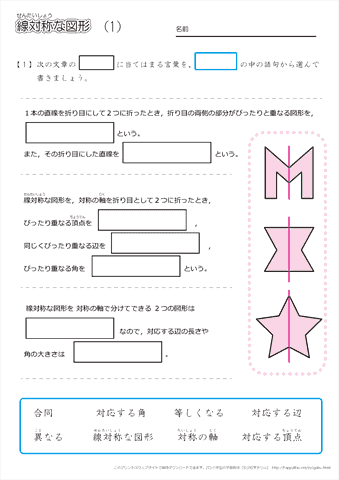
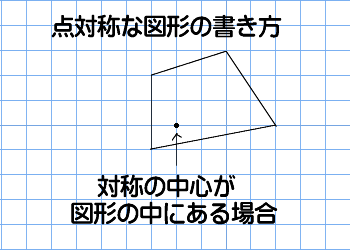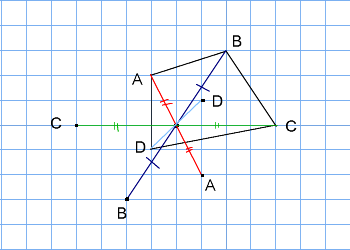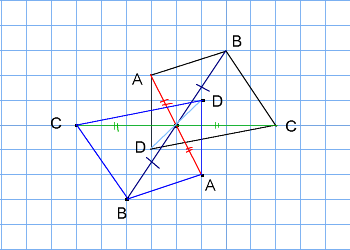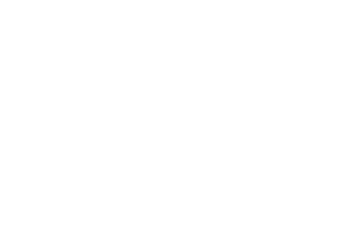
だから点対称の場合は中点を利用して求めよう。それが簡単だからね。 あと、点対称を求める場合は どの点に関して対称なのか 問題文をよく読もう。 「点\(\small{ \ \mathrm{A} \ }\)に関して対称」って言われたら点\(\small{ \ \mathrm{A} \ }\)が中点になるってことだからね。小学6年生の算数 線対称な図形 問題プリント 無料ダウンロード・印刷できる、線対称な図形の練習問題プリント です。 線対称な図形の意味と性質、図形さがし、作画などを練習し、理解を確かめることのできるプリントです。線対称・点対称の見分け方 図形の上に縦線を引く(イメージでOK) 図形を180°回転させる 線対称: 180°回転させるまでに左右対称になる瞬間がある(左右対称になった回数が対称の軸の本数) 点対称: 180°回転させた時、元の図形の形と一致する 左右
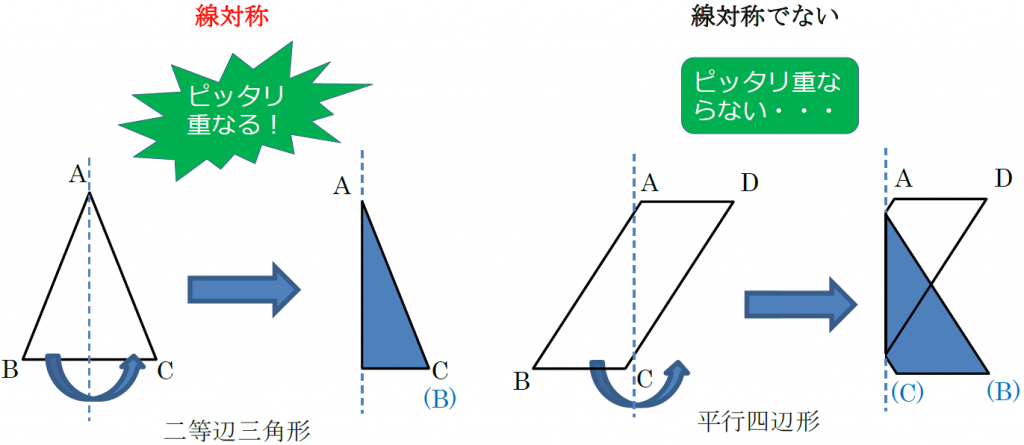
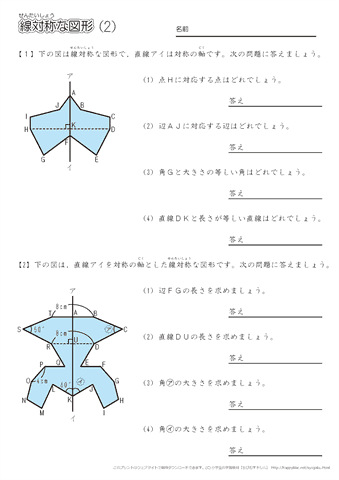
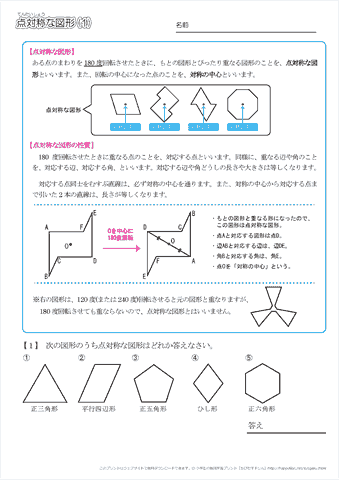
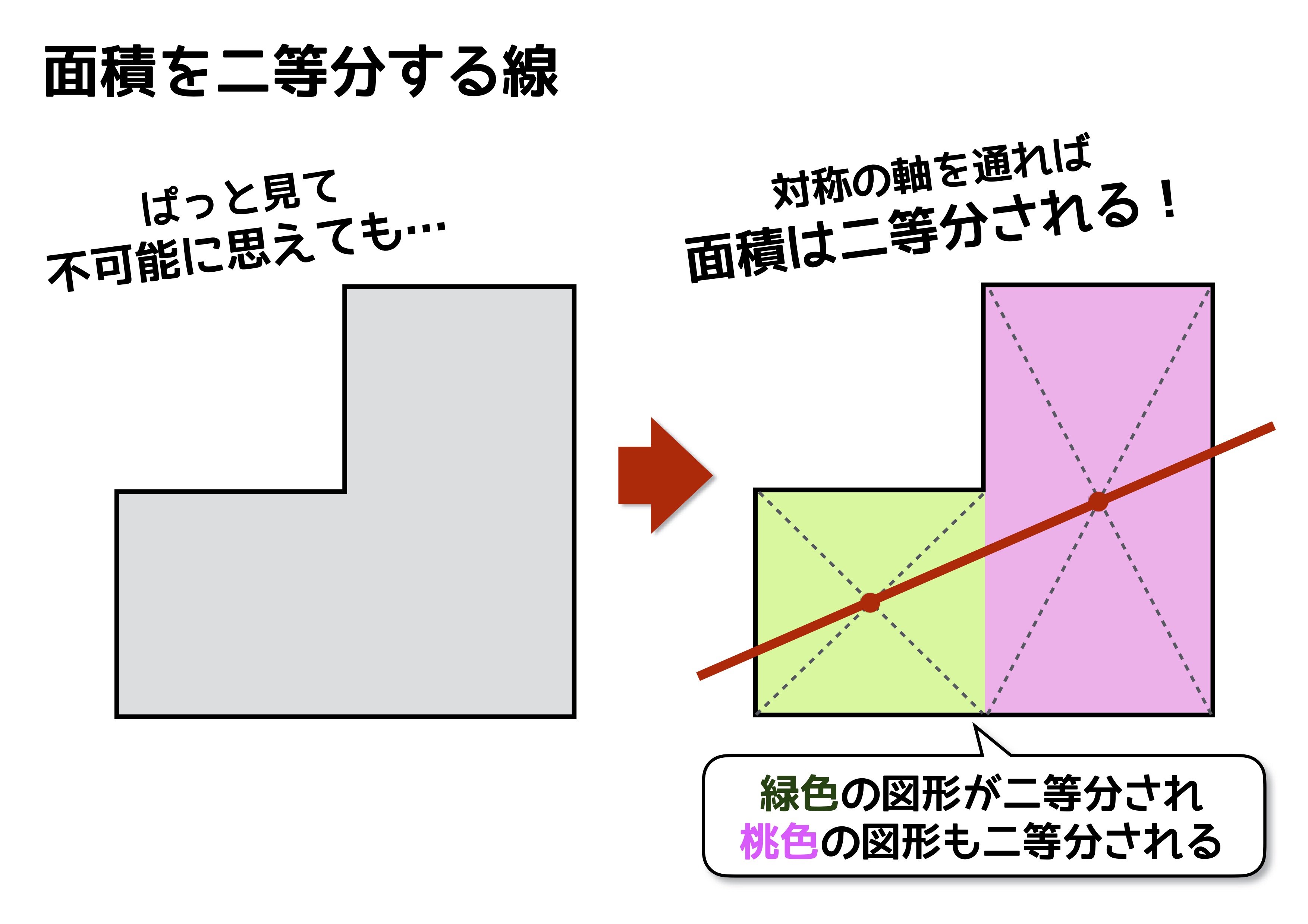
ある図形に対し、線対称、点対称は次のように定義されます。 ・線対称:ある直線を折り目にして折りたたんだとき、折り目の両側がぴったり重なること ・点対称:ある一点で180度回転させたとき、もとの図形とまったく同じ形になること この問題では 教科書とかを見てまとめてみました ( *´꒳`* ) 練習問題のページの答えのところは暗記シールを貼ってあります! 対称な図形 線対称 点対称 あおりんご この著者の他のノートを見る このノートが参考になったら、著者をフォローをしませんか? 気軽に 線対称な図形がもつ性質 を利用して解きましょう。 点Qの座標を求めるので、座標を定義しておきます。ちなみに点Qの座標は、 2直線の垂直条件 や 中点の座標 を利用するときに必要です。 点Qの座標を定義して、 2直線の傾き をそれぞれ求めます。
線対称 点対称 問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
 |  | |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
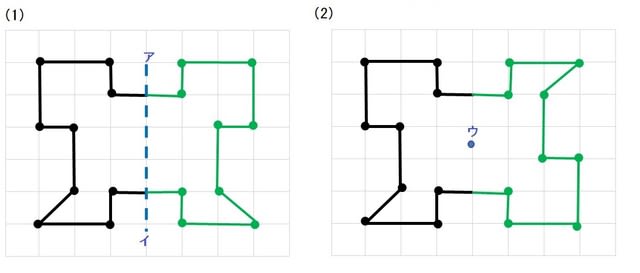 | 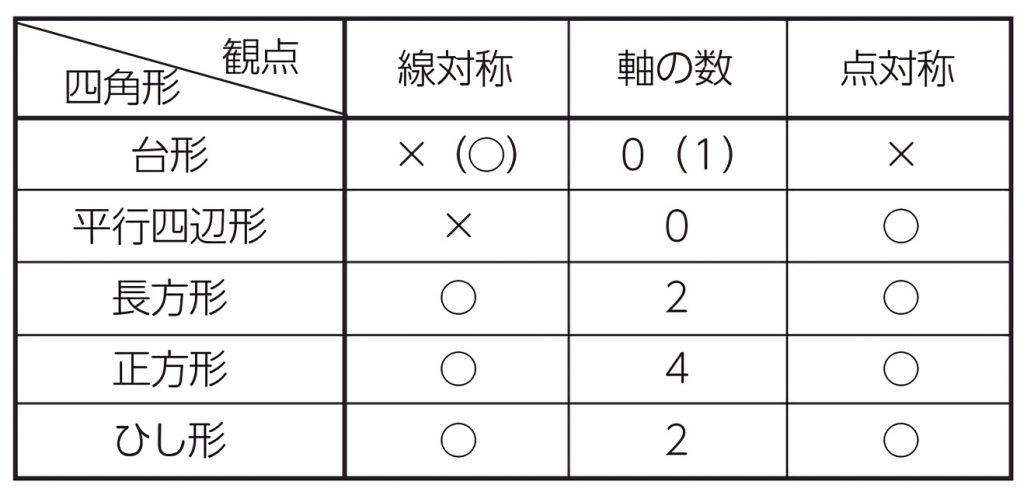 |
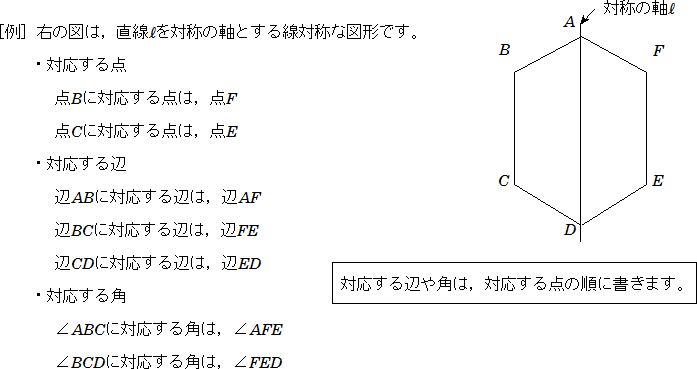
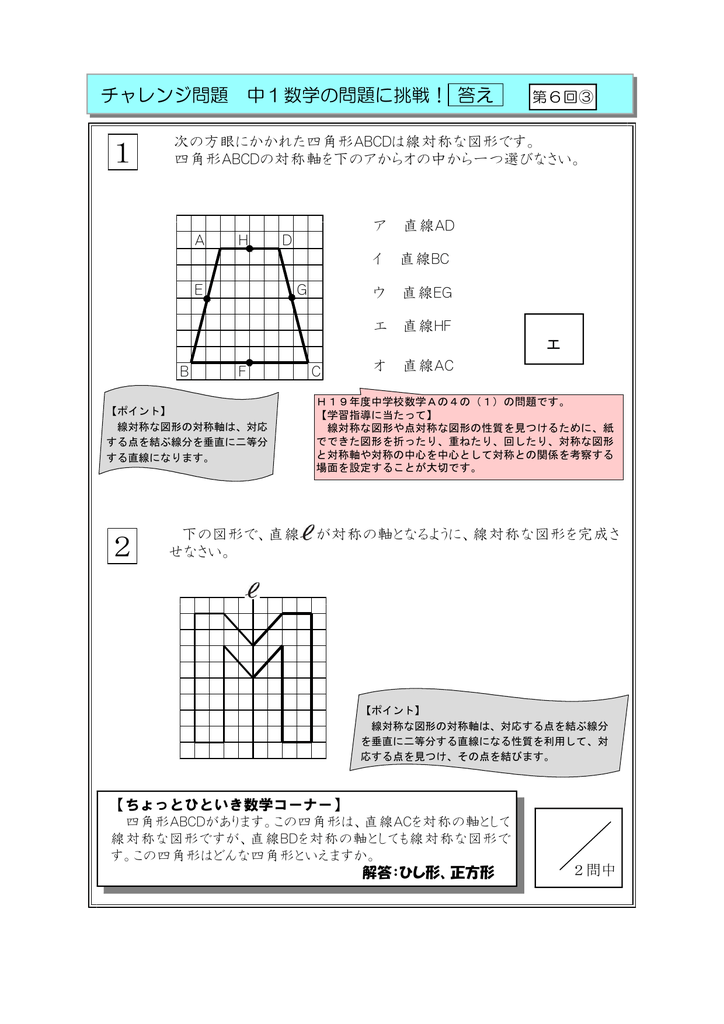
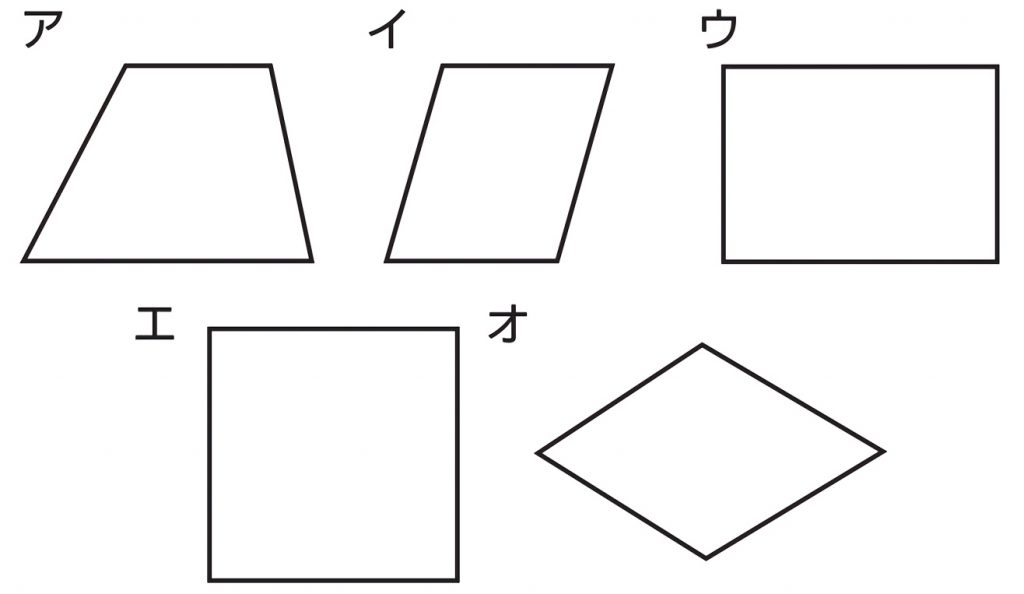
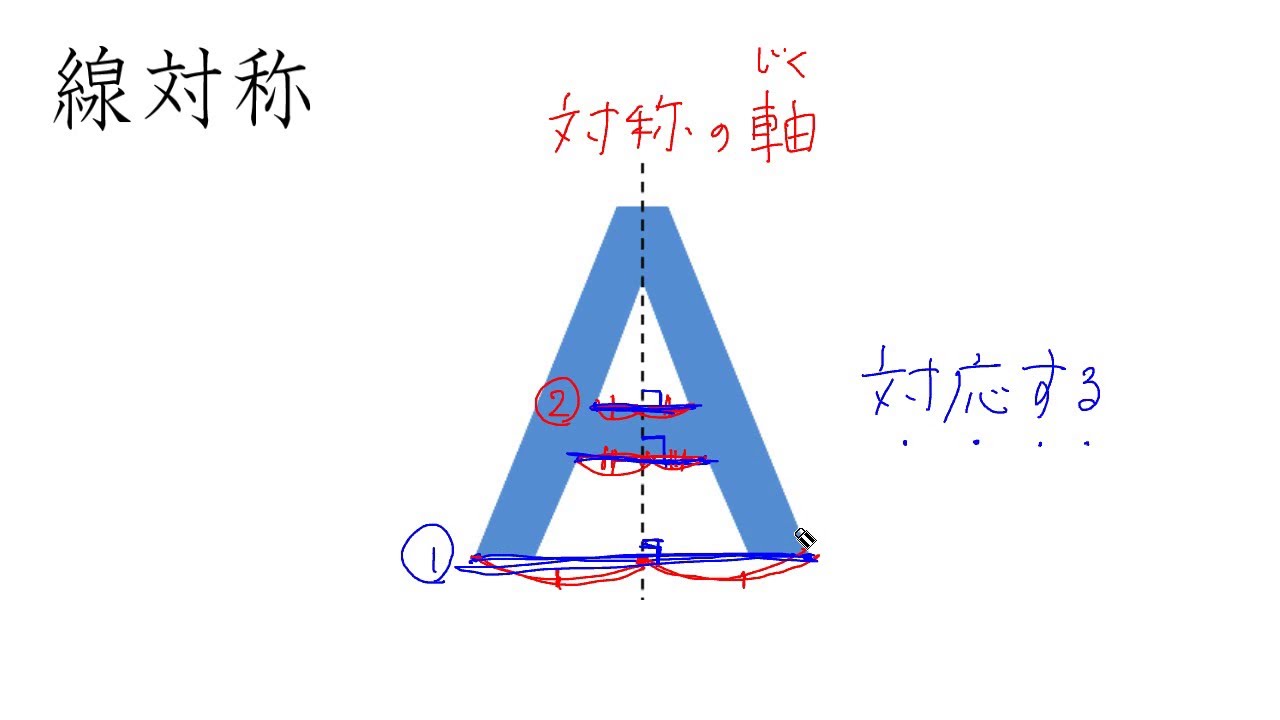
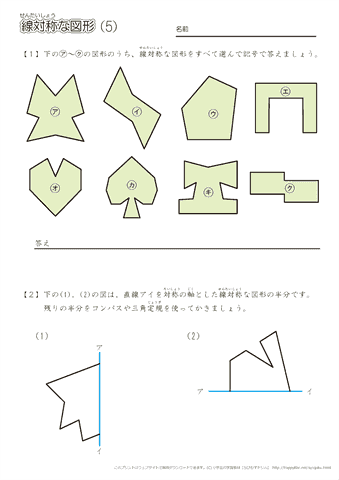
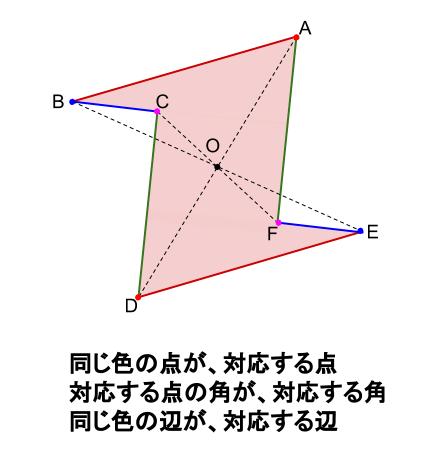
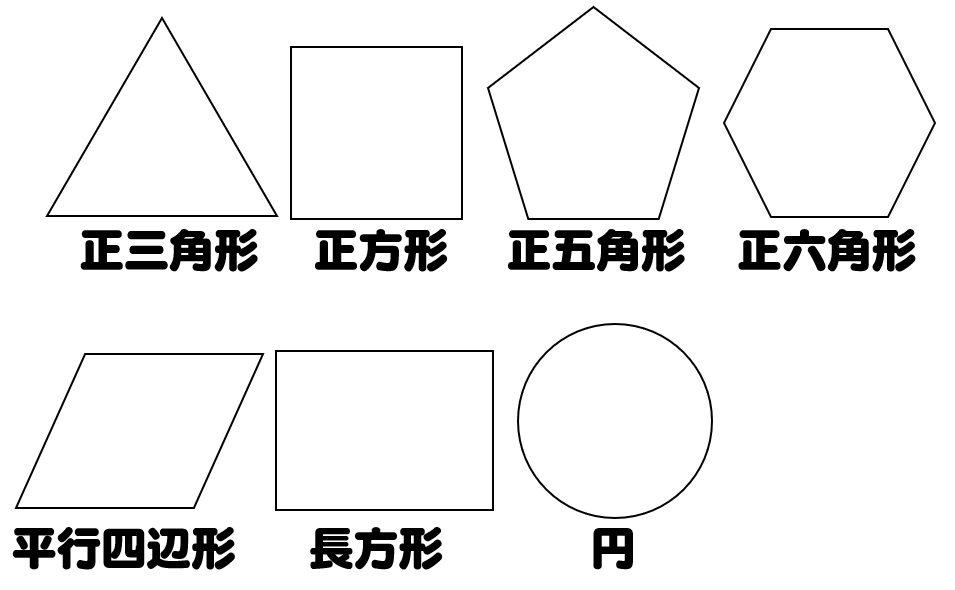
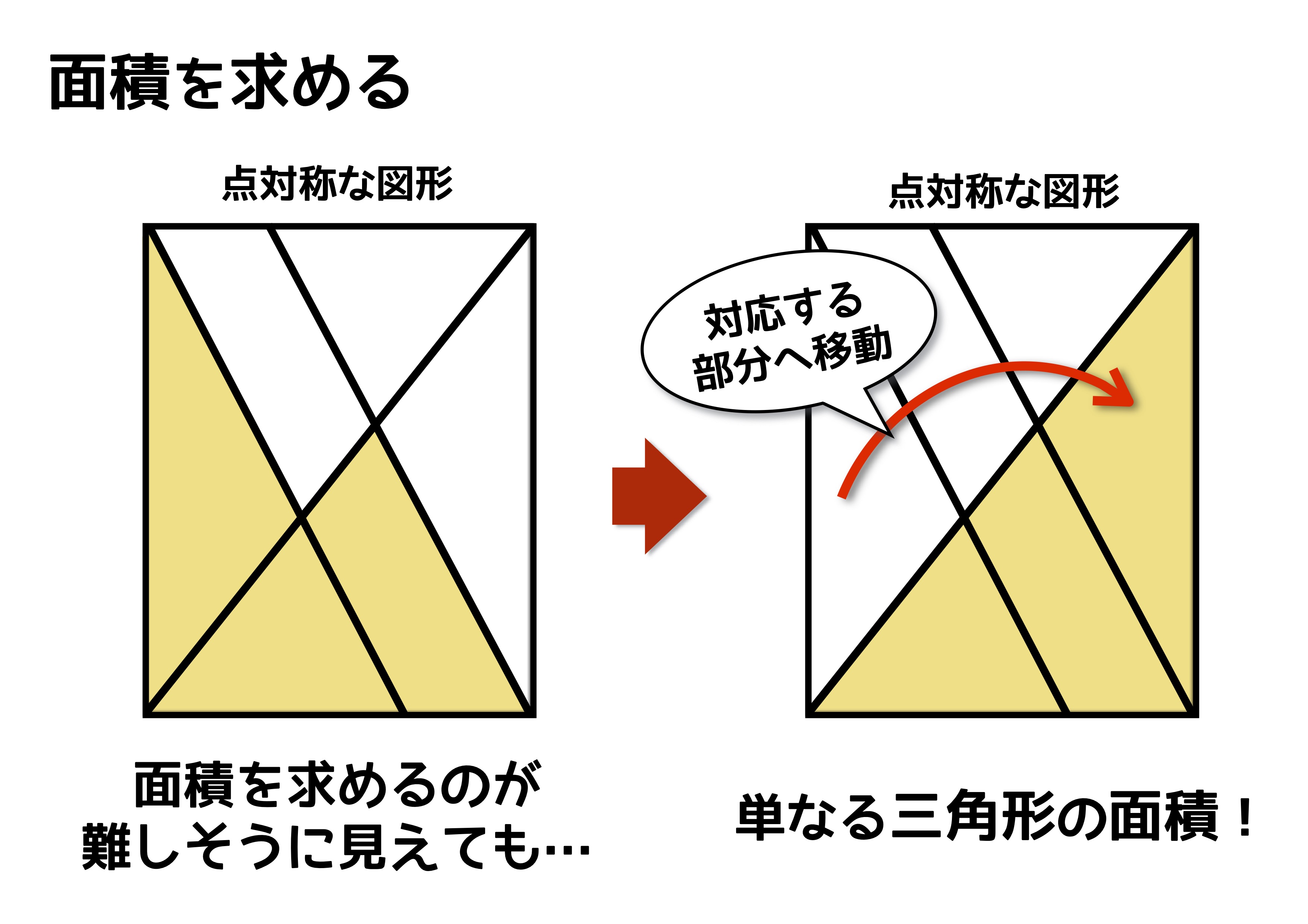
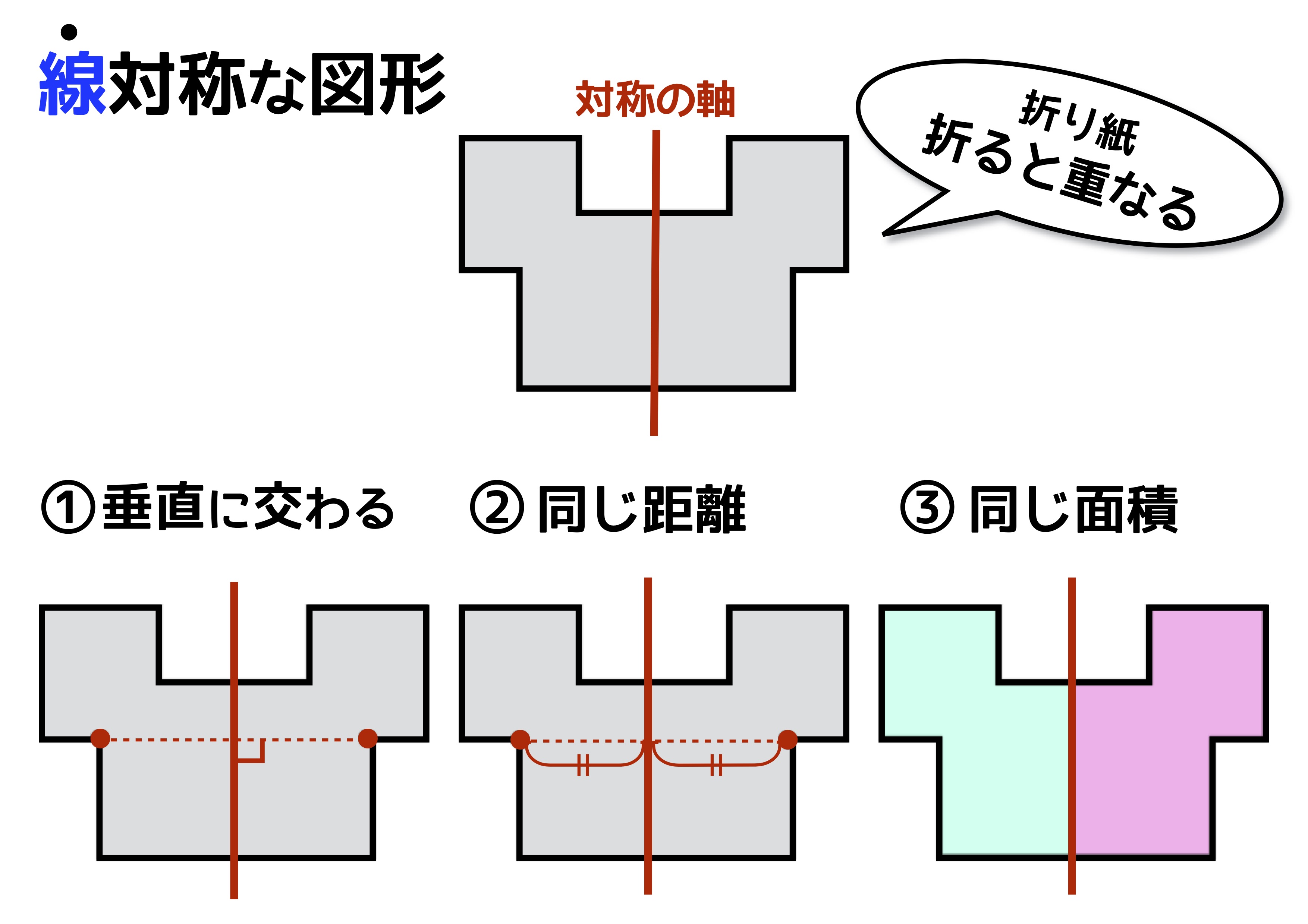
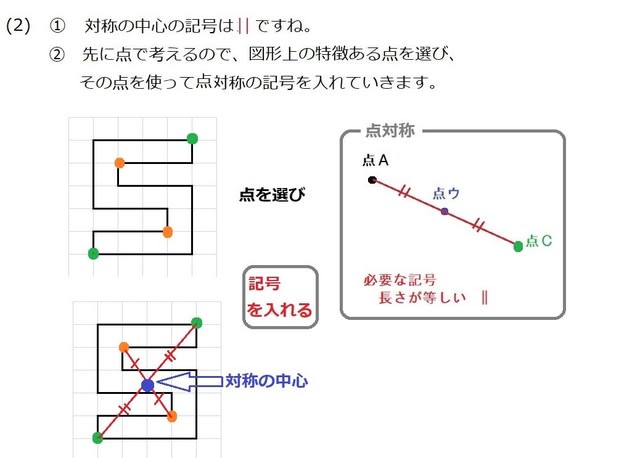
線対称 ア,イ,オ 点対称 イ,ウ,オ イとオは,線対称と点対称の両方にあてはまります。また,エ はどちらにもあてはまりません。 図1線対称な図形では,対応する点を結ぶ直線は,対称の軸 に垂直に交わります。対称の軸から対応する点までの長 問題 下の5つの四角形について、線対称な図形か点対称な図形かを調べましょう。 性という新しい観点から考察し、図形について理解を深めることをねらいとしています。線対称と点対称という観点を学習するとともに、これまで学習してきた平面図形
Incoming Term: 線対称 点対称 問題, 線対称 点対称 問題集,




0 件のコメント:
コメントを投稿